Everyone should be more-or-less familiar with the following two metrics that we commonly use in Machine Learning: F-score and G-mean. The F-score is defined as follows:

\[F=\frac{2*Pr*Re}{Pr+Re} = \bar{H}(Pr,Re)\]

which is the harmonic mean (\(\bar{H}\)) of precision (\(Pr\)) and recall (\(Re\)). Similarly, the somewhat less-known G-mean is another average of two very commonly used metrics; sensitivity (\(Se\)) and specificity (\(Sp\)):

\[\bar{G}(Se, Sp)=\sqrt{Se*Sp}\]

Here, a geometric mean (\(\bar{G}\)) is used. I couldn’t help but wonder: Why do we use the harmonic mean for precision and recall, while we use the geometric mean for sensitivity and specificity? It turns out, that this choice is not entirely arbitrary. Diving into this question was a useful exercise for me to understand these metrics better.

What are we measuring?

Before going into why we use one definition of mean over the other, let’s take a closer look at what we are actually trying to measure. We will be talking about the following scores:

• Precision is the number of true positives (TP), divided by all positive predictions (PP).
• Recall (or sensitivity) is the number of true positives (TP), divided by all actual positives (P).
• Specificity is the number of true negatives (TN), divided by all actual negatives (N).

And the following averages (for two inputs):

Harmonic mean: \(\bar{H}(x_1, x_2) = \frac{2*x_1*x_2}{x_1+x_2}\)

Geometric mean: \(\bar{G}(x_1, x_2) = \sqrt{x_1*x_2}\)

The usual argument

If you search on the internet “Why do we use harmonic mean for F-score?” you will typically find the same (somewhat unsatisfying) answer: if either precision or recall are zero, the mean will be zero too. Or conversely: both precision and recall have to be relatively high for the mean to be high. This is easy to verify just by looking at the numerator of the F-score: multiplying precision and recall have this effect. But wait - we could also just use the geometric mean¹ because it contains the same multiplicative expression. So why does it make (more) sense to use harmonic mean instead?

Harmonic mean preserves units

Typically you will want to use the harmonic mean when you are measuring the rate of something. Precision and recall both count the rate of true positives. The nice thing about applying the harmonic mean is that the result preserves the original unit: it is the rate of true positives over the total number of examined cases. Revisiting the F-score formula:

\[F=\frac{2*Pr*Re}{Pr+Re} = \frac{2TP}{2TP+FP+FN} \quad \left[\frac{\texttt{#TP}}{\texttt{#cases}}\right]\]

The right hand side of the equation becomes clearer when you look at a visual representation of what you are counting. It is the total number of true positive (\(2TP\)) predictions, over the number of positive samples (\(P=TP+FN\)) plus the number of positive predictions (\(PP=TP+FP\)). The result is the rate of true positives among samples that are either positive or predicted positive.

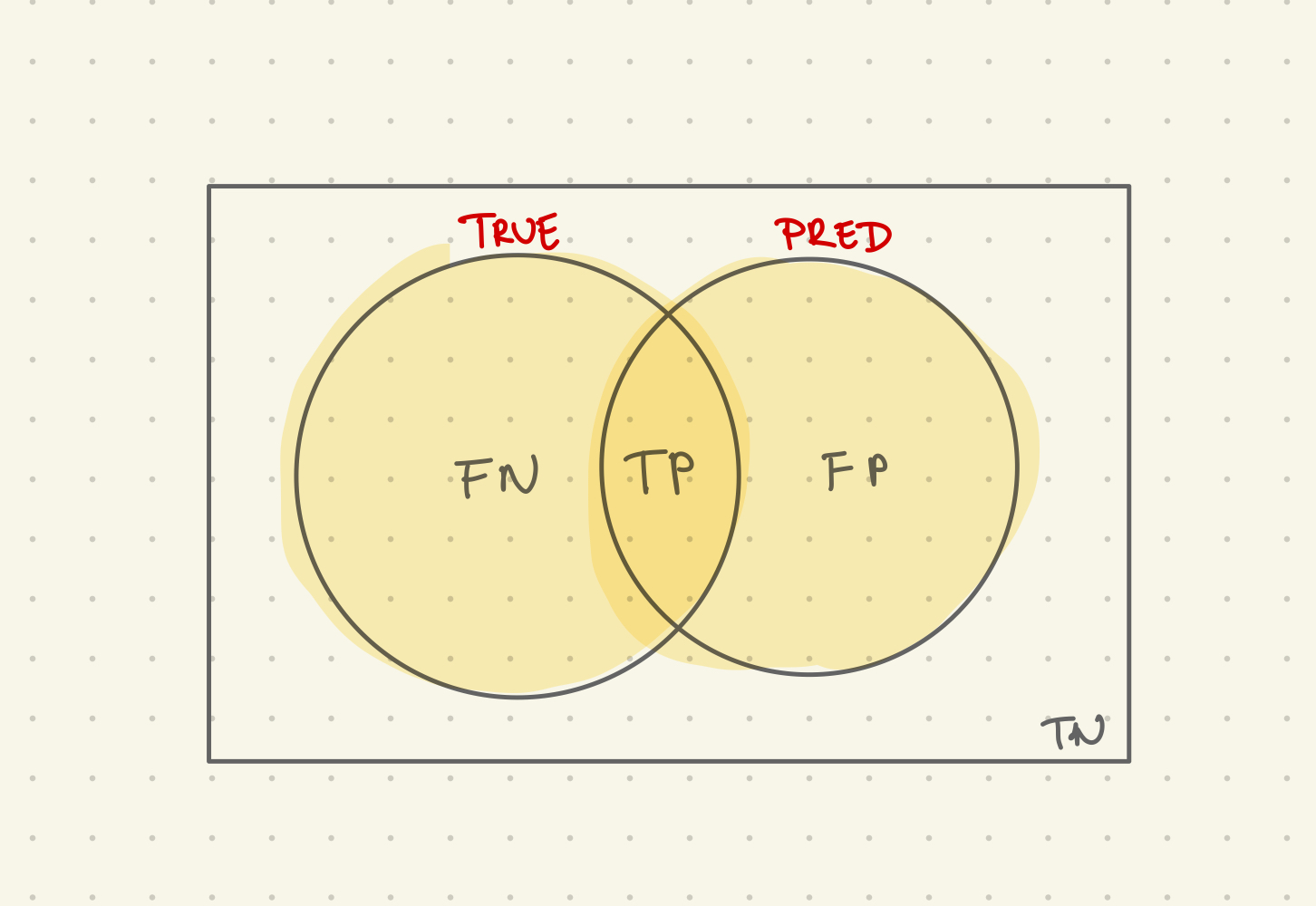
For precision and recall, it just makes sense to choose the harmonic mean over the geometric mean to preserve the original unit because it makes the result more interpretable. Sensitivity and specificity on the other hand measure the rate of two different things: true positives and true negatives. Here, we don’t have a common unit, so using either mean seems appropriate.

No deeper meaning

I don’t want to imply that choosing either mean over the other has a special meaning in Machine Learning. Usually, the average has an important connection to some total value depending on how we define it. ² For G-means, I don’t have an intuitive interpretation for the product of scores like sensitivity and specificity. If you do have in intuition for these total values in the context of Machine Learning, please let me know! But for now my conclusion is that the choice of means is not that deep.

When to use F-score or G-mean?

Notice that the F-score does not factor in the number of true negatives (\(TN\)). I would say that it is a useful metric when predicting the positive class correctly is more important for some reason. This is typically true for predicting diseases - you care about correctly predicting people with the disease correctly (who may represent 1% of the population). The F-score for the negative class is not meaningful in this highly imbalanced case, since a predictor saying no one is sick would have both very high precision and recall³. If you have an imbalanced dataset, and both classes are equally important, then the G-mean is probably a better choice.

Conclusion

• Harmonic mean preserves the unit
  • makes sense for F-score (rate of true positives)
  • otherwise, no reason to choose one over the other
• Use F-score when you care about correctly predicting the positive class
• Use G-mean when you care about both classes in an imbalanced dataset

---

Acknowledgements

Cover image source

Footnotes